

2 slit experiment
On the left is what is expected for this experience on the right is what actually happens, rather than getting Lines we get an interference pattern
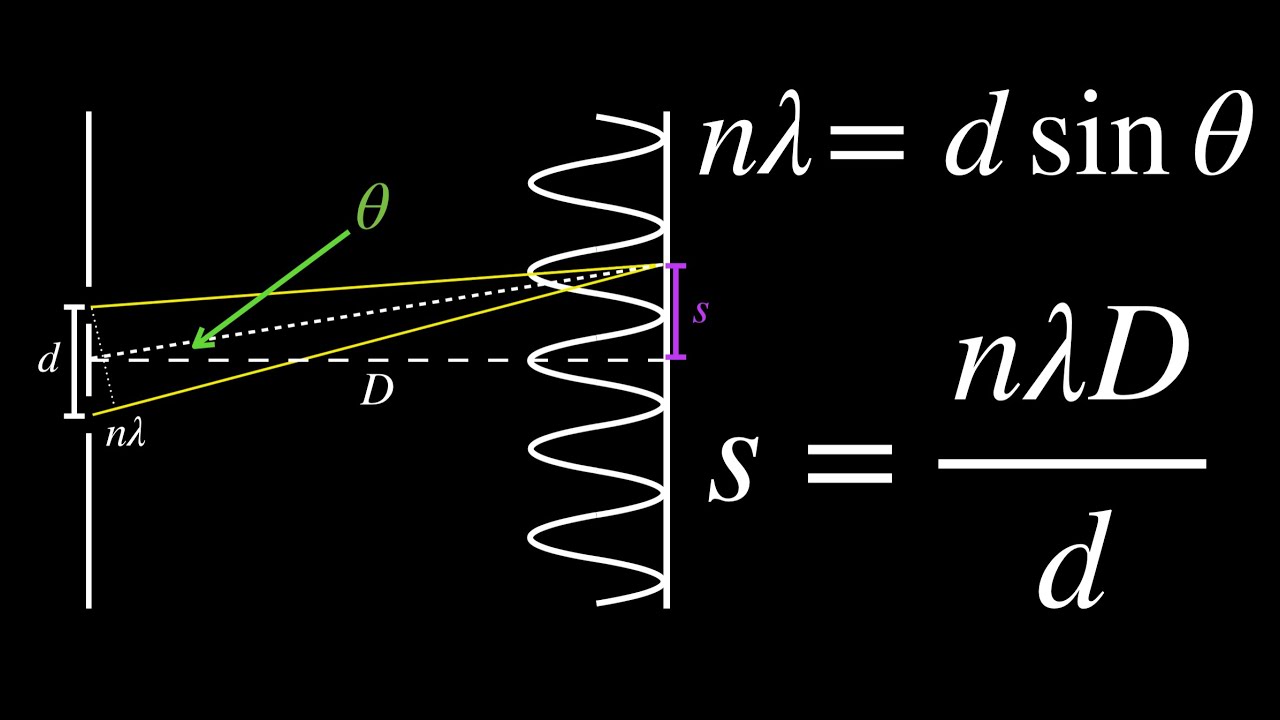
$$ \lambda p=h \\ E^2=\left(\frac{hc}{\lambda}\right)^2+m^2c^4 \\ \text{For photons: } E=\frac{hc}{\lambda} $$
$$ \psi (x,t) $$
Properties:
- $\psi$ is generally a complex number
- $\int|\psi|^2\,\text{d}x=\int\psi^*\psi\,\text{d}x =$ probability distribution
- $\left<x\right>=\int\psi^*x\psi\,\text{d}x=$ expectation value
- $\Delta x=\sqrt{\left<x^2\right>-\left<x\right>^2}=$ uncertainty
- The function needs to be normalised, meaning $\int^{+\infin}_{-\infin} |\psi|^2=1$
$$ \hat{p}=-i\hbar\frac{\text{d}}{\text{d}x} $$
$$ \left<p\right>=\int^{+\infin}{-\infin}\psi^*\hat p \psi\,\text{d}x=\int^{+\infin}{-\infin}\psi^*\left(-i\hbar\frac{\text{d}\psi}{\text{d}x}\right)\,\text{d}x $$
$$ \begin{aligned} \Delta x\Delta p &\sim \hbar\\ \Delta E \Delta t &\sim \hbar \end{aligned} $$
Wavefunction of a particle stuck in an Infinite well of width L in Red, and PDF of the wavefunction in green
We can find the wavefunction of a particle stuck in an Infinite well by taking the “Time independent Schrödinger equation”:
$$ -\frac{\hbar^2}{2m}\frac{\text{d}^2\psi}{\text{d}x^2}+V(x)\psi=E\psi $$